Hardware Signing for Ethereum

All popular blockchains, starting with Bitcoin through Ethereum all the way up to Zcash, use the Elliptic Curve Digital Signature Algorithm (ECDSA) for cryptographically signing transactions.

Software implementations of ECDSA may be susceptible to side-channel attacks that leak information about the private key. Luckily, the latest generation devices are equipped with specialized hardware that supports key generation and signing, but leveraging these new features for existing blockchains is not straightforward because of the different algorithms involved.

The work in this article was done on behalf of Trusted Key Solutions and is used in Trusted Key’s IDENTIFY secure digital identity system.

Cryptographic Signatures

A cryptographic signature proves that the sender of the transaction had access to a private key and that the transaction has not been changed since it was signed. These ECDSA signatures are typically calculated in the wallet app by first creating a digest (hash) over the unsigned transaction data and then running the EC digital signature algorithm to calculate a pair of 256-bit integers identified by ‘r’ and ‘s’. This pair of integers is added to the transaction data to create a signed transaction and then broadcast to the blockchain network.

000:
020:
040:
060:
080:
0A0:
0C0:
0E0:

version01000000Number of inputs01Unspent transaction hashac18fa31f68e5597d4d1580ec1bdea10be30a39d10dddfd41360b3
f7bbc40facUnspent output index00000000Length of scriptSig6aPush sig on stack47DER sequence30Length of sequence44DER integer02Length of integer206d3e58f553c0605c3a663d6baa7258cd53
6f3c50f4aac96c361695f82ab2017dValue of rDER integer02Length of integer2003ad05075cff6be0185d4dcc7581a6
0634de35a33585f009ab2f0d1beb9ccbd8Value of sSIGHASH flags01Push pubkey on stack21Pubkey (compressed)0374b22e7dd641b4d24c483023
a275fc808c813fe89f8cb4a9c97ef0f3431afb37Sequence numberffffffffNumber of outputs02Value (Satoshis)02000000000000
00Length of scriptPubKey19OP_DUP76OP_HASH160a9Push address on stack14Destination addressa24d41cca0b9baba81ce4f43747d97e24846ca60OP_EQUALVERIFY88OP_CHECKSIGacValue (Satoshis)ee3dcd1d00
000000Length of scriptPubKey19OP_DUP76OP_HASH160a9Push address on stack14Destination address44635889ad4ba11e76c14d347867c48dba4069b3OP_EQUALVERIFY88OP_CHECKSIGacLock time000000
00

Signed Bitcoin transaction (Pay2PubKeyHash); ECDSA signature in red (hover for info)

000:
020:
040:
060:

RLP with 1 size bytef8Size of RLP structure6dTransaction nonce21RLP length of gas price85Gas price0ba43b7400RLP length of gas limit83Gas limit2fefd8RLP length of address94Destination address54450450e24286143a35686ad77a7c851ada
01a0RLP length of value88Value (Wei)0de0b6b3a7640000Extra data (none)80Pubkey recovery bit1bRLP length of ra0c36fdbf8043a64a6096ee81da4de7f04def4
77b9a3210a18967fad07f72112b2Value or rRLP length of sa04aedfd1d9d9085256373b40ef02bc3da0a
95054f40075de340086c9512707b29Value or s

Signed Ethereum transaction (Ether transfer); ECDSA signature in red (hover for info)

The miners on the network then check the transaction details (whether you actually have money to spend, for example) and verify the ECDSA signature to ensure that the sender, identified by a public key, has had access to the corresponding private key. Multiple transactions are combined into a block, including a reference to the previous block, creating a chain of blocks.

Protecting the Private Key

It’s obvious to see that when somebody obtains a copy of your private key, he/she can calculate valid signatures over malicious transactions that will be accepted by the network as if they came from you. The security of your funds or smart contracts depends on the security of your private key(s).

There are several popular ways for securing your private keys to ensure they cannot be copied or stolen:

• Regenerating the private key using a Key Derivation Function (KDF)
• Using a Secure Element with hardware signing

A Key Derivation Function generates a private key from a secret value such as a password or passphrase. By regenerating the private key each time it’s needed, no key needs to be stored and therefor no key can be copied. However, the derivation algorithm itself can leak side-channel information that reveals the private key.¹

With hardware signing, the private key resides in the hardware and cannot be retrieved. It can only be used to calculate signatures. The private key and any temporary values calculated during signing reside in hardware registers and are not stored in memory or accessible from software. Of course, having unprotected access to the hardware would allow an attacker to sign malicious transactions all the same, without knowing the private key, so this method and KDF are often combined, with the derivation of the key happening in hardware as well.²

The latest Android and iOS devices support hardware signing on a specifically designed hardware component called the Secure Element. In the case of iOS, Apple has included its Secure Enclave since the iPhone 5S. Standalone Secure Elements that support hardware signing are also available from many vendors, including Atmel³, Infineon⁴, NXP⁵.

Unfortunately, neither the Android SDK nor the iOS 9+ SDK support the elliptic curve that’s used for the popular blockchains. This is indeed the reason why all cryptocurrency wallet apps are using software signing. Similarly, many of the hardware solutions mentioned earlier do not support the blockchain curve either. This means that it’s far from trivial to use hardware signing with any of the popular blockchains. Before we can dig into this some more, let’s see what elliptic curves actually are.

Elliptic Curves 101

This introduction to Elliptic Curve Cryptography (ECC) is heavy on algebra. Feel free to skip to the next section Curve Parameters.

An Elliptic Curve is an algebraic curve defined by the equation: y² = x³ + a⋅x + b

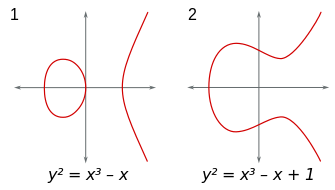
Two elliptic curves with different values for constants a and b

In the context of Elliptic Curve Cryptography, a private key is simply a random positive integer, typically identified with the letter d. The corresponding public key, identified by Q, is actually a point on the curve with coordinates (Qx,Qy). These coordinates are calculated by taking a base point on the curve, G for “Generator”, and multiplying it by the private key d. The coordinates of the base point (Gx,Gy) are also a constant and are chosen as to generate unique values with each subsequent addition.⁶

The term “addition” in this context is not the same as with integers but is defined as a new operation that takes two points on the curve and calculates a third point. Multiplication of a point by an integer (multiplication by a scalar) is no different than applying addition multiple times. In short, point Q (the public key) is calculated by adding point G (the curve’s generator) to itself d (the private key) times, Q=G+G+G+G+G+… or Q=d×G

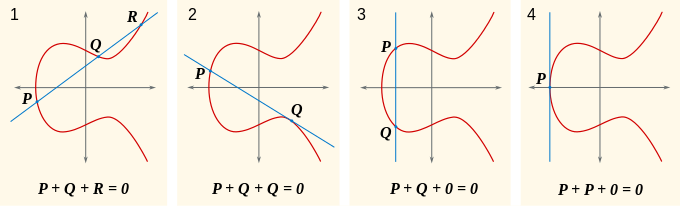
Definition of addition for a pair of points on an elliptic curve

The Elliptic Curve Digital Signature Algorithm (ECDSA) can be summarized as follows: the signer picks a random number k and calculates a point C on the curve using C=k×G. Using this random number, together with the signer’s private key d and the digest (hash) e from the message to be signed, the signer calculates a positive integer s=(e+r⋅d)/k. The final ECDSA signature (r,s) consists of r, the x-coordinate of C = Cx, and the calculated integer s. Given the message, the signature, and the signer’s public key, anybody can verify that the signer has had access to the private key and that the message is authentic. The security aspect of ECDSA stems from the fact that it’s easy to calculate a point on the curve by multiplication, but it’s near-impossible to derive the parameters that resulted to that point.

The last thing to note is that all calculations in ECC are happening over a “finite field”. What this means is that the all the values in the calculations are limited to use values from a finite set of numbers. In particular, for 256-bit ECC, all the parameters are limited to be from the set of positive integers smaller than some big number p, where p itself must be smaller than 2²⁵⁶ in order to make every value fit within 256 bits of storage.

Curve Parameters

There are many elliptic curves, with different parameters, that are being used for cryptographic purposes.⁷ Mostly for historical reasons, the different blockchains have settled on a curve called secp256k1 which has the following parameters:

p = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
a = 0
b = 7
Gx = 0x79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
Gy = 0x483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
n = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

Elliptic curve domain parameters secp256k1

As mentioned before, the different hardware solutions support multiple curves, but usually do not support secp256k1. Instead, they include support for a curve called secp256r1, also known as prime256. This also happens to be the only 256-bit curve that’s supported by the Android SDK hardware backed key store and iOS’s Secure Enclave. The question why these hardware solutions are using this particular curve and not the other popular one is a source of many conspiracy theories.⁸

p = 0xFFFFFFFF 00000001 00000000 00000000 00000000 FFFFFFFF FFFFFFFF FFFFFFFF
a = -3
b = 0x5AC635D8 AA3A93E7 B3EBBD55 769886BC 651D06B0 CC53B0F6 3BCE3C3E 27D2604B
Gx = 0x6B17D1F2 E12C4247 F8BCE6E5 63A440F2 77037D81 2DEB33A0 F4A13945 D898C296
Gy = 0x4FE342E2 FE1A7F9B 8EE7EB4A 7C0F9E16 2BCE3357 6B315ECE CBB64068 37BF51F5
n = 0xFFFFFFFF 00000000 FFFFFFFF FFFFFFFF BCE6FAAD A7179E84 F3B9CAC2 FC632551

Elliptic curve domain parameters secp256r1

Needless to say, it’s not possible to verify a signature calculated from one curve with an algorithm designed for another curve. A point calculated with one set of parameters would simply not lie on the curve represented by the other set. A public key calculated by secp256r1 hardware would not be a valid public key for use with Bitcoin, for example. We could still rely on the hardware backed APIs to evaluate the key derivation function and as a source of high-quality randomness. But having to run the signature calculation in software may expose the private key to side channel attacks from other programs running on the same processor, even across virtual machines.⁹

It’s worth noting that signing hardware is often versatile and can be configured for different curves. But even when the underlying hardware supports custom curves, the SDKs do not necessarily give 3rd party developers access to all these functions and usually limit ECDSA to secp256r1. This is currently the case for both Android and iOS.

Going Meta

Simply put, there’s no way to leverage the Android or iOS hardware signing functions to directly sign blockchain transactions. We can however sign transactions indirectly: by having a “man in the middle” that verifies the secp256r1 hardware signature and generating a compatible secp256k1 signature for the final transaction. “Man in the middle” is not usually a term one likes to hear when it comes to security, and for good reason. If the man in the middle can generate valid signatures on my behalf, what’s keeping him from generating signatures without my explicit consent? The end-to-end security of such a setup is completely dependent on the security of the middleman; the fact that I’m using hardware signing is not making it any more secure.

In the case of Bitcoin or Zcash, we’re out of luck. Without dedicated secp256k1 hardware support we are stuck with signing transactions in software.

In the case of Ethereum, however, we have at our disposal a Turing-complete secure virtual machine. We can verify the hardware signature in the virtual machine, no matter what signing algorithm was used to calculate it, as long as we can code up an implementation of the verification algorithm to run inside the Ethereum virtual machine.

Implementations of the ECDSA verification algorithm are a dime a dozen and too many to enumerate here. In fact, there’s already a tested and open source implementation for Ethereum by Vitalik Buterin, co-founder of Ethereum.¹⁰ From the constants in that code it’s apparent that it was written to verify signatures using the secp256k1 curve, as can be expected. It’s straightforward to change all the curve constants to their secp256r1 counterparts, according to the parameter lists above. Unfortunately, doing this did not work, and it’s not immediately apparent why it wouldn’t. Although, the fact that the code does not declare the constant a from the list is a solid hint.

Premature optimization is the root of all evil — Donald Knuth

As usual, the devil is in the details. From the curve parameters you can see that for the secp256k1 curve the parameter a is 0. This means that the secp256k1 curve equation can be simplified as y² = x³ + 7, completely dropping the a⋅x term. The algorithm in the ecc.se file has been optimized to exclude any multiplication that involves a. And this optimization is not unique to this code. It just so happens that lately, most open sourced ECDSA code that’s available on the internet was written for blockchain wallets and these all have the same or similar optimizations. Changing their constants from one curve to the other does not work.

What is needed is an algorithm that is generic enough to be applicable to all curves, yet still contains the usual optimizations that make ECDSA feasible in the first place. (Imagine calculating a public key naively by actually adding a curve point to itself ~2²⁵⁶ times; it would simply take too long.) Furthermore, the code must be general enough to allow for easy porting to a language that Ethereum understands.

In the end we’ve settled on porting an implementation of ECDSA written by Sébastien Martini in 2010 called wcurve.¹¹ His Python code supports both secp256r1 and secp256k1 curves and is very friendly to porting to Solidity and Serpent: the major programming languages of Ethereum. It would make sense to port the Python code to Serpent, since the Serpent programming language was based on Python in the first place, but lately a lot of the tooling around Ethereum is being built for the newer Solidity programming language, a JavaScript lookalike. Alas, when we tried two months ago, the Solidity compiler could not handle the ported algorithm and the compiler consistently threw an exception on a not-implemented code path deep within its optimizer. We were stuck with the older, less feature filled, Serpent compiler.

Our Wcurve contract¹² allows anyone to verify secp256r1 signatures by invoking the contract’s ecverify method. The contract was compiled with Serpent version bffd9be and deployed to main net at address 0x1a7706D9b3D6253e8135A48c39CA01B6B470C943. Simply include the below ABI spec into your contract and you can call it from your own code. The code doesn’t (yet) support the public key recovery that’s included in the Ethereum built-in ecrecover, so the caller will have to provide the full public key as arguments Qx and Qy.

secp256r1 Wcurve on main net at 0x1a7706D9b3D6253e8135A48c39CA01B6B470C943

secp256r1 Wcurve on testnet at 0x17523499561B901dC3B7e6af84B5fb53765E1326

The Wcurve contract ABI definition can be found below. Note that this ABI definition can be reused for 256-bit curves other than secp256r1.

contract Wcurve {
    function ecverify(uint256 Qx, uint256 Qy, uint256 e, uint256 r, uint256 s) constant returns(bool);
}

Wcurve ABI definition for Solidity

contract WcurveTest
{
    Wcurve wcurve;
    function WcurveTest(address wcurveAddress) {
        wcurve = Wcurve(wcurveAddress);
    }
    function testR1(bytes32 Qx, bytes32 Qy, bytes32 r, bytes32 s) returns(bool)
    {
        bytes32 e = sha256("user should have signed this string");
        if (wcurve.ecverify(uint(Qx), uint(Qy), uint(e), uint(r), uint(s)) == false) {
            return false;
        }
        // do something useful
        return true;
    }
}

Using Wcurve from a Solidity contract

abi=[{name:"ecverify",type:"function",constant:true,inputs:[{name:"Qx",type:"uint256"},{name:"Qy",type:"uint256"},{name:"message",type:"uint256"},{name:"r",type:"uint256"},{name:"s",type:"uint256"}],outputs:[{type:"bool"}]}]

Wcurve ABI definition for web3

wcurve=eth.contract(abi).at("0x17523499561B901dC3B7e6af84B5fb53765E1326")

Using the pre-deployed Wcurve contract with web3 on testnet

wcurve.ecverify("0x4bd613713cd1282639f74c758d76b46dd683aec8b0fcd7018ce190725d5558c7","0x94e5582fb9d1b6bf3696fb926ee859f20f091817ebd350f6318dc25afc5afae5","0x0e177fa9a997f02c0e0d378ee12bf38034dcf2eb2ad4da30121985ee20562c14","0x97d637ec960950ebe62ba2a48c1bf8bd2a22dac8e757dfc00e13ac77667b5032","0x9191060fda370fcc773936fe759555ebd21134d97f39a617007eba8ba799586f")

Example web3 Wcurve invocation using a valid secp256r1 signature

Conclusion

We encourage everyone to leverage our Wcurve contract to add secp256r1 support to their own contracts. Hopefully this can serve as an initial step to getting a built-in secp256r1 version of Ethereum’s ecrecover.¹³

We welcome comments at the Wcurve GIST page¹², by e-mail at lionello <AT> enuma.io, or on reddit.

References